Hi there, I'm writing this blog because probability is a part of my master's syllabus so, I wanna share my learnings here.
Note:
$$3x + 2a = 5^2$$
❌don't follow this approach, like writing raw math equeations
✅ Instead use words,sentences, clarity, honesty, justification, & thinking.
Probability
Probability is a branch of mathematics that studies the possible outcome's likelihood and its distributions.
In common usage, the word "probability" means the chance that a particular event or set of events will occur.
It is expressed on a scale of 0 - Imposibility to 1 - Certainity.
It can also express in percentages between 0% and 100%
Random experiment
A random experiment is a process of observing the outcome of an event.
Outcome
The outcomes are all possible results of the random experiment.
Sample Space (S)
The sample space is the set or collection of all the outcomes of an experiment and is denoted by capital "S".
ex:
Random experiment is rolling a dice.
Output might be 1,2, or 3, till 6.
sample space S = {1,2,3,4,5,6}

Complement of Event
The complement of event A is the set of all outcomes in a sample space that are not included in event A.
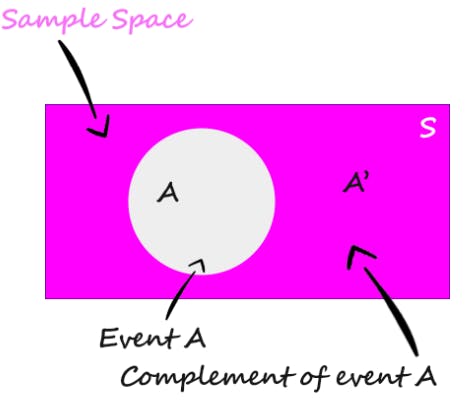
The complement of event A is denoted by A'.
👉 Union of A and A'(complement of A) is equal to sample space S.
$$A \cup \overline A = S$$
👉 Sum of probability of A and A' is equal to one.
$$P(A) + P(\overline A) = 1$$
👉 Probability of complement of event A is equal to subtracting probability of envent A from one.
$$P(\overline A) = 1 - P( A)$$
Intersection, Union, and complement of events
Intersection of Events
The intersection of events A and B is the event that both events A and B occur.
Denoted by A intersection B 👇
$$A \cap B$$

Note: A intersection B &B intersection A both are same.
$$A \cap B = B \cap A$$
Example
Event A: Person doing an Internship
Event B: Person pursuing MS
Out of 12 persons, seven are doing an internship, five are pursuing MS, and out of twelve, three are doing both.
So the intersection of events A and B is 3. Because three persons are doing both events(occurs) at the same time, doing an internship along with MS.
Mutually Exclusive Events
Look at the Venn diagram, where A and B do not overlap.
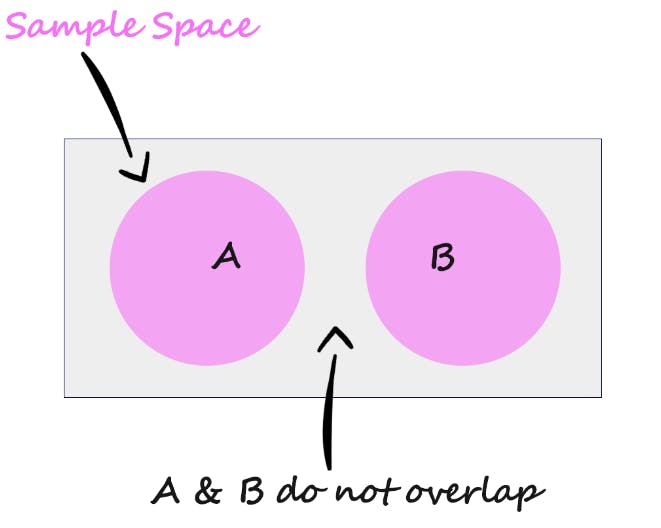
They have no intersection. But formally we can say that intersection of event A and event B is the empty set.
Their intersection contains no elements.
In simple words, mutually exclusive events mean they do not occur at the same time.
Example
Event A: Sunrise
Event B: Sunset
Here events A and B are mutually exclusive events because they do not occur at the same time.
And the probability of their intersection is zero.
$$P(A \cap B) = 0$$
Union of Events
The union of events A and B is the event that either A or B or both occurs.
Denoted by 👇
$$A \cup B$$
or we can say A or B.
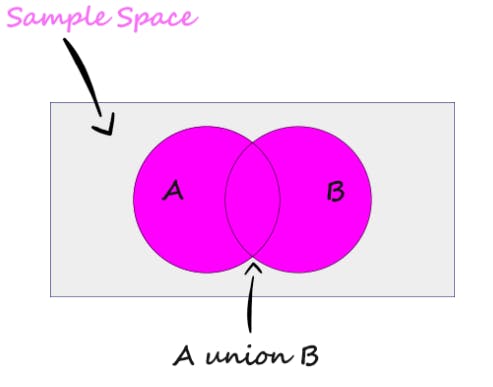
When we use the term A or B in probability, we are referring to their union.
And using the word or in the inclusive sense A or B means A or B or both.
$$A \cup B = B \cup A$$
The probability of the union of two events can be found with the addition rule
$$P(A\cup B) = P(A) + P(B) - P(A\cap B)$$
Conclusion
These are the few concepts from where we can start our journey to Probability.
I hope you find this blog helpful.
Thanks for reading 👍

